Post by Luigi FortunatiPost by wugiPost by Luigi Fortunatihttps://www.geogebra.org/m/dzuyjaz6
Your simulation may be more or less correct, but it doesn't help much in
one's understanding it correctly, it even may induce erroneous
understanding.
First, it should be made clear in which direction the moving observer is
supposed to move. My first impression was that he should move vertically
which didn't make sense.
- observer B moves (instantaneously) to the right, i.e. towards body C
- observer A is stationary with respect to body C
- Observers A and B, at time t=0 of both, share the same space and the same time
- The time of C in the reference of A is different from the time of C in the reference of B.
Post by wugiFurthermore, it doesn't help to superpose both 'circles' in a same
graph, which suggests a same reference frame, where in fact different
reference frames are superposed. Now it gives the impression that "there
are two circles in space", one for each observer.
The fact is that there is only one object, but that both observers "fill
in" the space towards it, and the time values, differently! In order to
respect the singleness of the object, your method is not a very proper
one. There are better alternatives. One is, to make two graphs, each
with its reference frame. Another one, to display only one object, say
in the rest system, and superpose the different reference frame of the
moving observer upon that, showing the length contraction, and possibly,
time dilation effects.
Lastly, this is not what the observers are going to *see*! Einstein's
Lorentz equations don't describe objects *as seen*, they describe
*measured*, backcalculated, positions of simultaneity. What the
observers are going to see, is what the light photons are telling them,
as they arrive at each observer, come from the different parts of the
distant object. In other words, they include Doppler distortions!
Ok, let's talk about what happens when photons of light arrive on the
photographic film (the observer) and form the image.
Are Einstein's Lorentz equations able to predict whether the body C will
appear perfectly spherical or whether it will be squashed in the
direction of motion?
[[Mod. note -- Yes.
As wugi noted, (1) and (2) below are very different questions, with
(1) What are the coordinate positions of the objects measured (i.e.,
"backcalculated", as wugi quite correctly terms it) in different
(inertial) reference frames, as determined by the Lorenz transformation?
(2) What image(s) would taken by a (ideal) camera located at a certain
point given (1) together with differential light-travel-time effects
(i.e., the Lampa-Penrose-Terrell effect, often just called the Terrell
effect or Terrell rotation)?
(1) is what's usually meant when we ask what an observer "measures" in
special relativity. (2) is what you (Luigi) have now asked about.
See
https://en.wikipedia.org/wiki/Terrell_rotation
for a nice introduction to (2). Reference 4 in that Wikipedia article
(written by Victor Weisskopf!) is a very clear exposition of the effect,
explicitly working out the Terrell rotation for a moving cube and then
generalizing it to an arbitrary-shaped body. The original 1960 paper is
(still) behind a paywall :(, but as of a few minutes ago google scholar
finds a free copy.
-- jt]]
Thank you. About Terrell rotation, if I remember correctly it would seem
to alledge that length contraction is part of the "seeing" effects, in
that the object, together with its backside becoming visible, would seem
rotated, and total length "seen" would be preserved. This is messing up
what I call "Lorentz" data (measuring, backcalculating: length
contraction) with "Einstein" data (*seeing, watching* , the back side
becoming visible).
But it is partly true. From my webside which I mentioned in another
reply, let's see some examples here.
How would a frontline that's approaching an observer at relativistic
speed be perceived? Here:
Loading Image...
(fat dot = observer, dotted line = actual 'true' position, rightmost
curve = as seen 'now', others = previous positions.)
Same case, after having past by the observer:
Loading Image...
(doppler 'blue shift' at approach, 'red shift' at regression)
A series of frontlines combined into a "squadron" of squares:
Loading Image...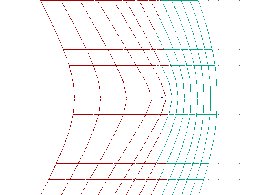
(dots = actual position of the squad)
Notice the following "seeing/watching" effects:
At approach, a "length dilation" is seen, not a contraction!
At regression, an extra length contraction is seen.
This is due to the fact that light needs the longest time to reach the
observer from the farmost parts of the moving object.
The squares appear more or less distorted, according to position and
distance from observer. This is analogous to, and more general than,
what Terrell rotation tries to tell us.
But observe this! ->
The true *Lorentz length contraction can be seen*, but only
perpendicular to the motion, and far enough away: in our picture, along
the vertical through the observer point, at the far distances up and
down (compare with dot positions).
I'd promised some other links to the effects of 'seeing' relativistic
motion. Here are some:
https://www.physicsforums.com/threads/terrell-revisited-the-invisibility-of-the-lorentz-contraction.520875/page-4
(with nice animations by J. Doolin)
https://www.tempolimit-lichtgeschwindigkeit.de/ueberblick/1
(with links to more videos)
https://www.spacetimetravel.org/tompkins/tompkins.pdf
(with other cases)
https://timms.uni-tuebingen.de/tp/UT_20040806_001_sommeruni2004_0001
(a lecture with animation videos of previous cases)
--
guido wugi